编者按

本文介绍半正定规划（SDP）的一些应用实例，也包含了一个基于Julia/JuMP使用Mosek求解器的计算实例。通过这篇文章，你将从0/1二次规划出发，了解SDP的理论和建模求解思路。

文章作者：覃含章

责任编辑：覃含章

文章发表于微信公众号【运筹OR帷幄】：优化 | 半正定规划(SDP)的形象理解和基本原理

一SDP实例和一些参考资料

SDP有很多有意思的实例，除了作为其特例的线性规划（linear programming），比如可以用来刻画线性系统（linear system）的李雅普诺夫稳定性(Lyapunov stability)，可以用来近似0/1二次规划（binary quadratic programming）的解，可以用来近似求解图上的独立集（independent set）/图的shannon capacity，带有特征值的优化问题（eigenvalue optimization），复数域上的插值（interpolation）问题，欧式空间上点的embedding问题，近似求解矩阵补全/带有nucelar norm的优化问题。

实际上，SDP作为一类特殊的凸优化问题，有很强的modeling能力。作为目前的研究来说其实更大的瓶颈是在计算，如如何找到泛用的大规模求解SDP的算法。因为虽然SDP从conic programming的角度来说和LP很像，但是实际上目前对它的一般结构并没有很好的了解。不像LP，一个实数域上finite dimensional的polyhedron我们是知道一定由有限个extreme points和extreme rays生成的（这也是著名的Minkowski Resolution Theorem），但对semidefinite cone我们就没有这样一般化的结构性定理。

那么不扯远了，我这边就不再一个个例子回答，因为如果想要了解如何用SDP去model上述的那些问题并近似求解，看一些参考文献就很快能比较好的了解了。这里先推荐一些参考读物。

对SDP零基础，但有一点点凸优化基础的同学（毫无优化基础的同学就先从Boyd, Vandenberghe的凸优化书入手）都可以从这份Robert Freund的讲义入门SDP，内容非常简明精悍，同时包含丰富的实例。

Introduction to Semidefinite Programming (SDP), by Robert Freund

（https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-251j-introduction-to-mathematical-programming-fall-2009/readings/MIT6_251JF09_SDP.pdf）

数学更好一些的同学，尤其是代数学的比较好的同学，想致力于SDP理论研究的，可以学习Pablo Parrilo等人的参考书。

Semidefinite Optimization and Convex Algebraic

Geometry（http://www.mit.edu/~parrilo/sdocag/index.html）

Prof. Parrilo主页上也有课程6.256/18.456 – Algebraic techniques and semidefinite programming的一些讲义、作业资料，可以配套学习。矩阵补全问题作为SDP可应用的一个实例，我在以前的知乎回答也有简单介绍：

矩阵补全（matrix completion）的经典算法有哪些？目前比较流行的算法是什么？（
https://www.zhihu.com/question/47716840/answer/110843844）

关于如何利用SDP近似计算独立集，以及SDP和copositive program的关系，可见我之前的一篇知乎文章：

覃含章：Copositive Programming简介（
https://shimo.im/docs/j7jWAf7fshQJm3NR/read）

之后我们就以SDP目前一个最为重要的应用为例，在binary二次规划（BQP）中来探讨如何理解SDP，并且如何利用SDP导出近似算法。之后的内容基本都源于Prof. Parrilo的讲义资料。

二Binary二次规划和半正定松弛

BQP的一般形式为，对一个n维的半正定矩阵 Q：

那么注意到这边的约束其实也可以写成 n 个二次方程 X²=1，也就是说原问题其实也可以看成是一个连续优化问题，一个polynomial optimization问题。

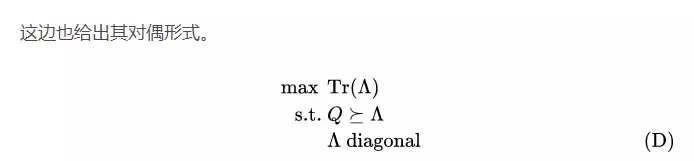
关于对偶形式，当然最直接的推法是通过对原SDP (P) 使用拉格朗日对偶。那么这边我们其实可以稍微灵活一些，我们可以直接对原来的BQP问题进行所谓的拉格朗日松弛（Lagrangian relaxation），这样让大家可以更深刻的体会拉格朗日对偶可以用来一般化地对（非凸）连续最小化优化问题求出一个下界。

而这就是我们前面的对偶形式(D)！

本节最后我们再给出一个概率解释。这个解释是针对SDP在原空间上的表达式的，也就是说跟前面lifting的解释更加相关。我们考虑现在不是确定性地找出最优的 x，而只是说需要随机地选取 x，使得期望上我们的结果比较好就可以了。那么我们BQP的目标函数就变成

三基于SDP的BQP近似算法的bounds：Goemans-Williamson, Nesterov, Grothendieck-Krivine

那么我们就意识到这里的 Q 其实是有比较好的结构的，比如理论上来说它有一个很好的特性：对角占优（diagonally dominant），这样使得我们的BQP的目标函数具有可分离的结构。

所谓的Goemans-Williamson rounding就是说对SDP松弛得到的解（可能是分数）再化整（round)成-1或1。这是SDP早期，包括到如今为止最成功和漂亮的应用之一。因为要知道的是，再1995年他们的paper发表之前，人们的各种非SDP方法最好就是只能达到0.5近似而且“卡壳”了许多年，他们基于SDP的方法一下子就将原来的0.5突破到了约0.878。

即我们基于SDP的Goemans-Williamson rounding能给我们期望上约0.878的一个近似算法！

注意这边的结果比之前是要糟糕的，因为左边是个等号。另外，不那么容易注意的一点是，前面两种rounding如果碰到SDP直接给出了一个全是 ±1 的解（最优解），rounding是不会干扰这个解的（虽然值可能会变，但仍然是最优的），而这边的话，即使已经有了一个最优解，一旦这个Grothendieck-Krivine rounding一用上马上就会把解变差！ （具体原因留给大家思考）

这边说点题外话，Grothendieck（是的，就是你知道的那位神一般的Grothendieck。当然，这里出现名字的所有人都已经够神的了）这里出现的相关的工作当然不是用来做BQP,SDP的（那会儿SDP的理论根本都还没有呢），他只是年轻的时候在做分析的时候顺便做了这么个结果。后来是被Krivine捡出来并用在这个bipartite结构的BQP问题里面了。为了给足Grothendieck credit，把这边相关的常数就叫做Grothendieck constant了。

对本节出现的分析的完整细节感兴趣的同学可参阅Parrilo相关讲义和书籍，或者其实还有个非常艰深的凸优化讲义（我所知道的所有凸优化教材里最为艰深的：Lectures on Modern Convex Optimization， by Aharon Ben-Tal and Arkadi Nemirovski）和其中所引用的相关文献。

四G-W rounding对一般化BQP问题的计算实例

注意我们进行10000次抽样，看看结果。

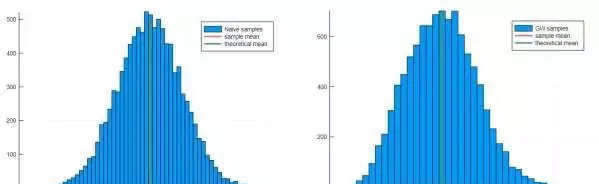
稠密Q的实验结果。左边：naive算法；右边：G-W rounding

那么我们确实看到G-W rounding计算得到的结果比naive的要好得多，在我这次实验中G-W rounding最优解的目标函数值是-5563.56而naive算法10000次下来最好也才得到了一个-1500左右的函数值。而且10000次取样的情况下我们的样本均值和理论均值也非常接近了，在我这次实验中，naive算法的样本均值和理论均值为16.21，19.26，而G-W rounding的样本均值和理论均值为-4879.23和-4880.3（所以图上基本都是一条线，肉眼看不出之间的gap）。

最后我们也对稀疏的 Q 和低秩（low rank）的 Q 看看G-W rounding的表现。我们从下图看到G-W rounding给出的解全部挤在一块了！（当然，10000次实验并不完全是同一个解，只是>95%都是同一个，所以直方图肉眼来看就塌缩成一条光杆了…）

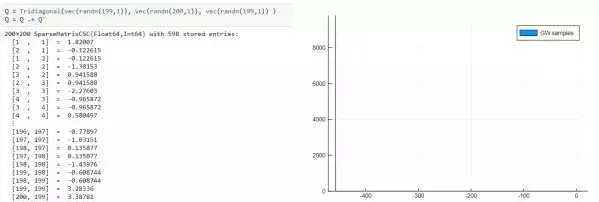
稀疏Q（这里选取了一个三对角对称阵）的实验

低秩Q（这里的秩为1）的实验

这个结果其实也应该是和直觉相符的，这里具体原因就留给大家作为思考了。提示：考虑在这种 的情况下真正所需要的超平面的维数？